Reduction

Introduction

A reduction is a method of deriving a single value from an array of values. For example, the summation of an array. A parallel reduction is a technique of coordinating parallel threads to produce the right results. The reduction can be defined for mathematical operations like addition, subtraction, min, max, multiplication, etc. This blog post will start with reduction trees, a simple reduction kernel, minimizing control divergence, minimizing memory divergence, minimizing global memory accesses, hierarchical reduction, and thread coarsening for reduced overhead. Let’s dig in!

This blog post is written while reading the tenth chapter, Reduction, of the incredible book “Programming Massively Parallel Processors: A Hands-on Approach¹” by Wen-mei W. Hwu, David B. Kirk, and Izzat El Hajj.

Reduction Trees

A reduction tree is actually a parallel reduction pattern whose leaves are original input elements and whose root is the final result. A reduction tree is not a tree data structure. Here, the edges share the information between the operations performed. For N input values, log2N steps are taken to complete the reduction process. The operator should be associated with the conversion from the sequential reduction to the reduction tree. We will also need to rearrange the operation while writing code; hence, the operator should hold the commutative property. Here’s an example of a typical parallel sum reduction tree:

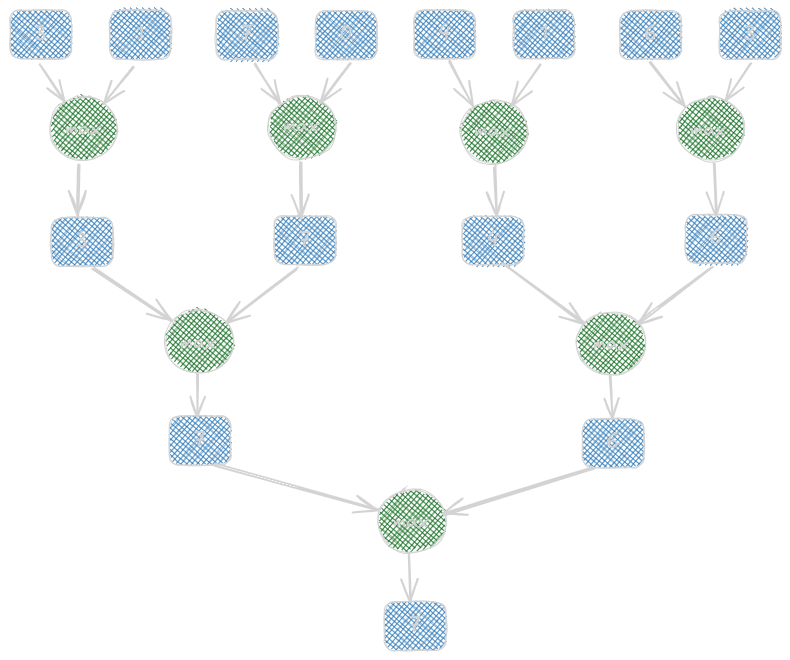
A Simple Reduction Kernel

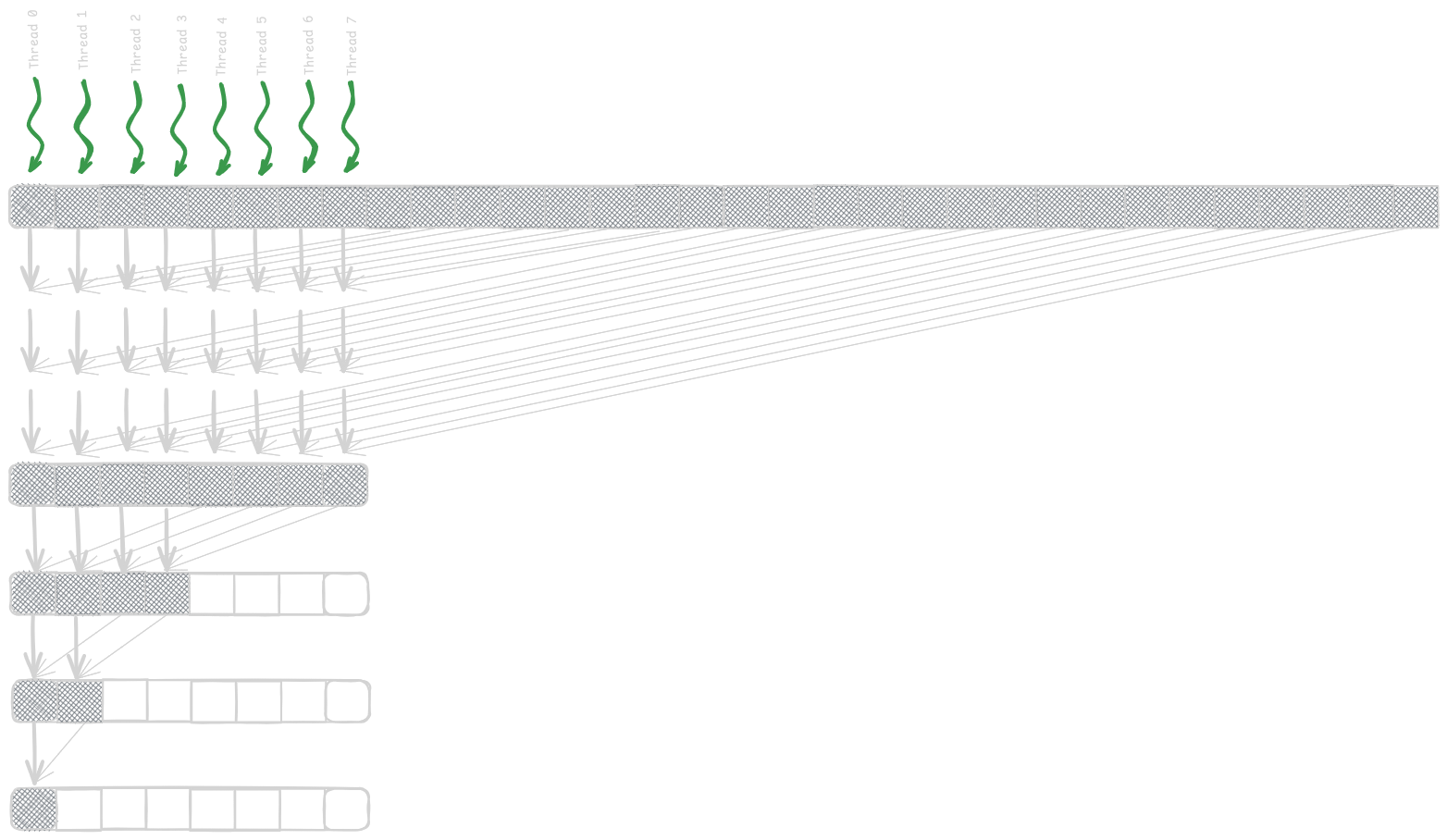
We will implement a parallel sum reduction tree such that reduction is performed within a single block. If the input block size is N, we will call a kernel and launch a grid with one block of 1/2N threads since each thread adds two elements. In the next subsequent step, half of the threads will drop off; now, 1/4N threads will participate. This thread will go on until only one thread is remaining to produce the total sum.

The figure below shows the assignment of the threads to the input array locations and their execution over time.

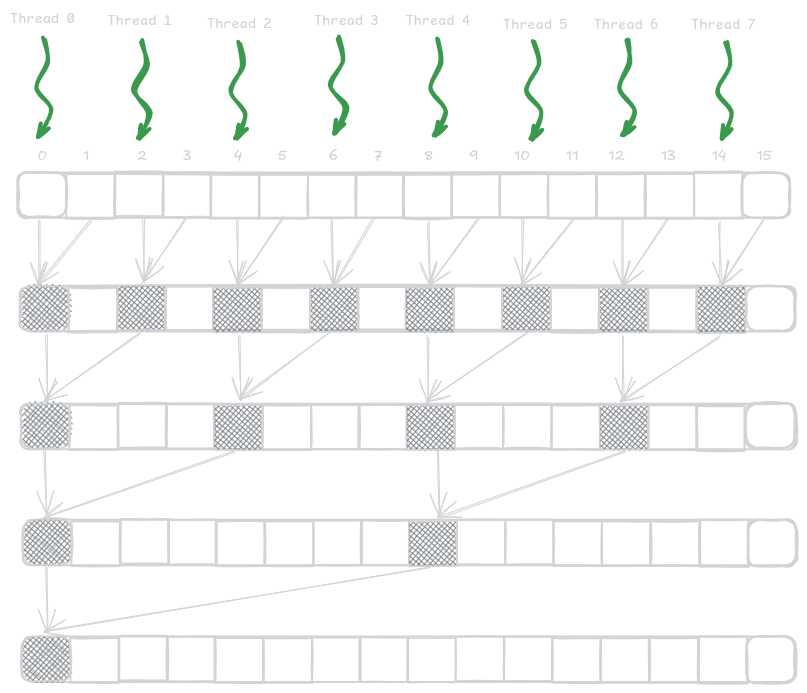
__global__ void simpleSumReductionKernel(float* input, float* output) {
    // note: it jumps 2
    unsigned int i = 2*threadIdx.x;
    for (unsigned int stride = 1; stride <= blockDim.x; stride *= 2) {
        if (threadIdx.x % stride == 2) {
            input[i] += input[i + stride];
        }
        __syncthreads();
    }
    if (threadIdx.x == 0) {
        *output = input[0];
    }
}

Minimizing Control Divergence

In the above method, managing active and inactive threads in each iteration results in higher control divergence because only half of the threads are used in the process, and half is wasted in the subsequent steps. This leads to a reduction in execution resource utilization efficiency. Hence, we need a better way to assign threads to the input array locations. In the above method, the distance between active threads increases over time, hence increasing the level of control divergence. There is a better way to do this. As time progresses, instead of increasing the distance between threads (strides), we should decrease them (as shown in the figure below). This will increase the efficiency and will improve the reduced resource consumption.

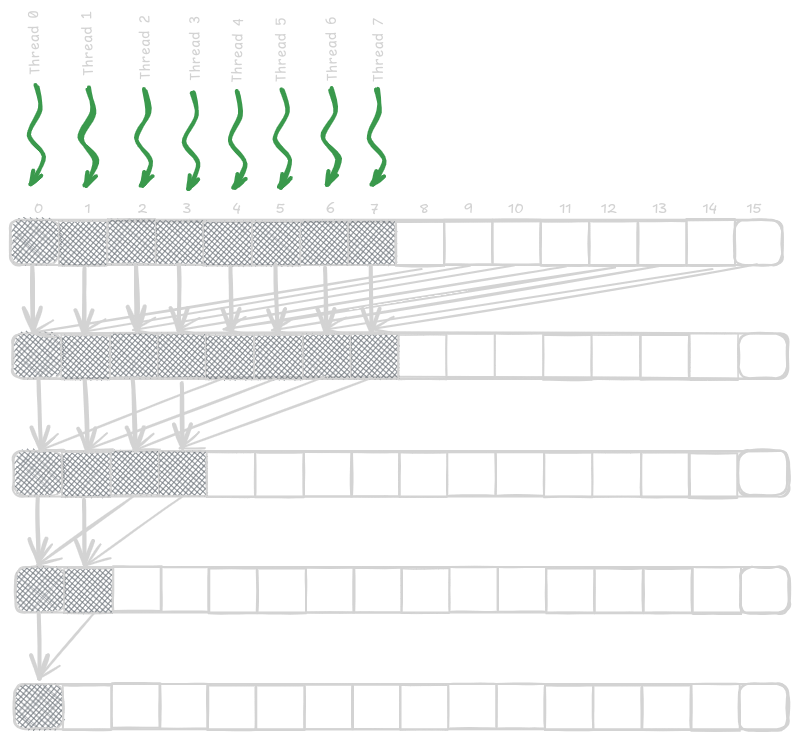
__global__ void ConvergentSumReductionKernel(float* input, float* output) {
    unsigned int i = threadIdx.x;
    for (unsigned int stride = blockDim.x; stride >= 1; stride /= 2) {
        if (threadIdx.x < stride) {
            input[i] += input[i + stride];
        }
        __syncthreads();
    }
    if (threadIdx.x == 0) {
        *output = input[0];
    }
}

Minimizing Global Memory Accesses

Following the above discussions, we can further improve performance by using shared memory accesses instead of global memory. We’ll keep the partial sum results in shared memory, as shown in the figure and code below.

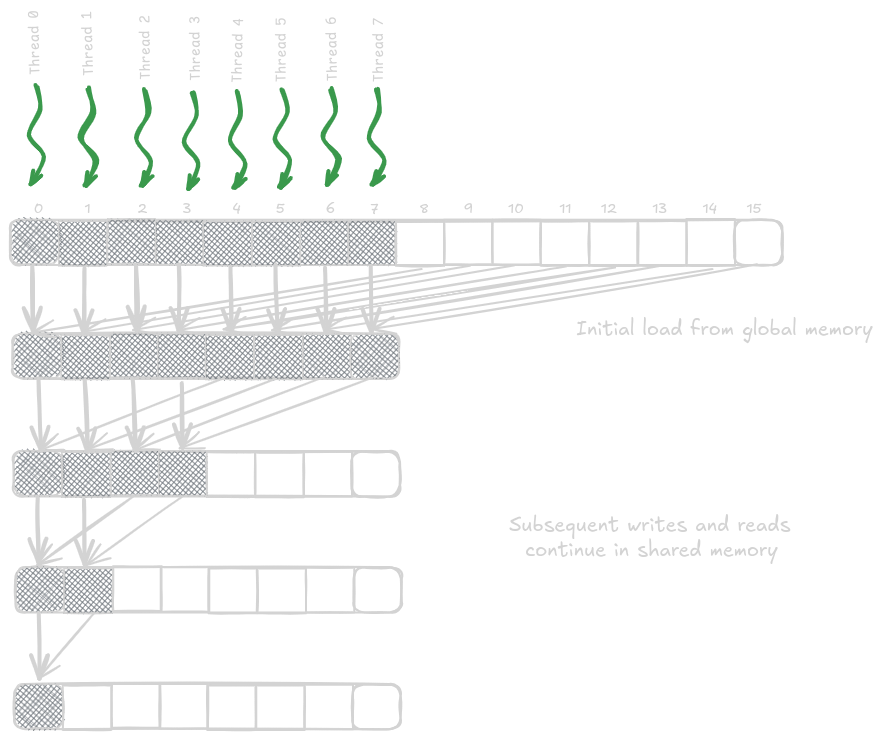
Note that for an N element input array, there will be just N + 1 global memory accesses. With coalescing, there will be N/32 global memory accesses.

__global__ void SharedMemorySumReductionKernel(float* input) {
    __shared__ float input_s[BLOCK_DIM];
    unsigned int t = threadIdx.x;
    input_s[t] = input[t] + input[t + BLOCK_DIM];
    for (unsigned int stride = blockDim.x/2; stride >= 1; stride /= 2) {
        __syncthreads();
        if (threadIdx.x < stride) {
            input_s[t] += input_s[t + stride];
        }
    }
    if (threadIdx.x == 0) {
        *output = input_s[0];
    }
}

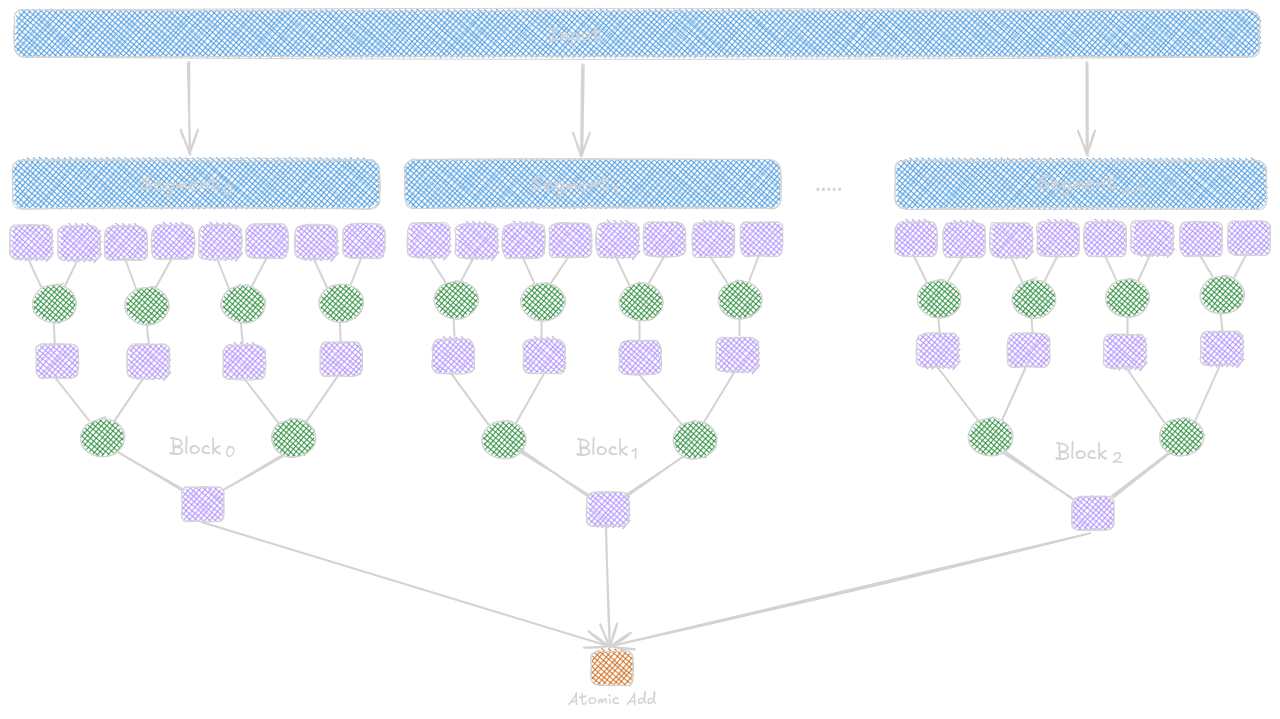
Hierarchical Reduction for Arbitrary Input Length

All the kernels above perform the reduction in a single block because we perform __syncthreads() operations which are limited within the block scope. This limits the level of parallelism to 1024 threads on current hardware. Things get slower when the input size increases. To resolve this, we partition the input elements into different segments such that each segment is the size of the block. Then, all blocks independently execute the reduction tree and accumulate their results for the final output using an atomic add operation.

__global__ SegmentedSumReductionKernel(float* input, float* output) {
    __shared__ float input_s[BLOCK_DIM];
    // each block process 2*blockDim.x elements
    // starting location of the segment to be processed by the block
    unsigned int segment = 2*blockDim.x*blockIdx.x;
    unsigned int i = segment + threadIdx.x;
    unsigned int t = threadIdx.x;
    input_s[t] = input[i] + input[i + BLOCK_DIM];
    for (unsigned int stride = blockDim.x/2; stride >= 1; stride /= 2) {
        __syncthreads();
        if (t < stride) {
            input_s[t] += input_s[t + stride];
        }
    }
    if (t == 0) {
        atomicAdd(output, input_s[0]);
    }
}

Thread Coarsening for Reduced Overhead

Until now, to parallelize reduction, we have actually paid a heavy price by distributing the work across multiple thread blocks. This process increases the hardware underutilization as more wraps start becoming idle, and the final wrap experiences more control divergence. Hence, we’ll serialize the thread blocks manually so that the hardware resources are not spent here. We’ll use the thread coarsening technique to do that and start by assigning more elements to each thread block.

The kernel code for implementing reduction with thread coarsening for the multiblock segmented kernel is given below.

__global__ CoarsenedSumReductionKernel(float* input, float* output) {
    __shared__ float input_s[BLOCK_DIM];
    unsigned int segment = COARSE_FACTOR*2*blockDim.x*blockIdx.x;
    unsigned int i = segment + threadIdx.x;
    unsigned int t = threadIdx.x;
    float sum = input[i];
    for (unsigned int tile = 1; tile < COARSE_FACTOR*2; ++tile) {
        sum += input[i + tile*BLOCK_DIM];
    }
    input_s[t] = sum;
    for (unsigned int stride = blockDim.x/2; stride >= 1; stride /= 2) {
        __syncthreads();
        if (t < stride) {
            input_s[t] += input_s[t + stride];
        }
    }
    if (t == 0) {
        atomicAdd(output, input_s[0]);
    }
}

Where to Go Next?

I hope you enjoyed reading this blog post! If you have any questions or suggestions, please feel free to drop a comment or reach out to me. I’d love to hear from you!

This post is part of an ongoing series on CUDA programming. I plan to continue this series and keep things exciting. Check out the rest of my CUDA blog series:

1. Introduction to Parallel Programming and CPU-GPU Architectures
2. Multidimensional Grids and Data
3. Compute Architecture and Scheduling
4. Memory Architecture and Data Locality
5. Performance Considerations
6. Convolution
7. Stencil
8. Parallel Histogram
9. Reduction

Stay tuned for more!

Resources & References

1. Wen-mei W. Hwu, David B. Kirk, Izzat El Hajj, Programming Massively Parallel Processors: A Hands-on Approach, 4th edition, United States: Katey Birtcher; 2022
2. Lecture 9 Reductions by Mark Saroufim; Mar 2024
3. I used Excalidraw to draw the kernels.