Performance Considerations
Introduction
The aim of the blog posts is to explain how to achieve high-performance computing. We need to manage parallel code alongside the given hardware resources. We’ll read about the off-chip memory architecture and discuss memory coalescing, memory latency hiding, and thread coalescing (which depends on the different aspects of the architecture). Lastly, we’ll study the common checklist of optimization techniques for different types of parallel patterns.
This blog post is written while reading the sixth chapter, Performance Considerations of the fantastic book “Programming Massively Parallel Processors: A Hands-on Approach1” by Wen-mei W. Hwu, David B. Kirk, and Izzat El Hajj.
Memory Coalescing
Memory coalescing is a technique used to move data efficiently from global memory to shared memory. It is used alongside the tiling techniques. When accessing the DRAM location, the range of consecutive locations that are along with the requested locations is accessed. These are known DRAM bursts. If any applications need any focused use of data, DRAM accesses them directly and transfers them at high speed, compared to some random access from the sequence.
In modern DRAMs, we know that the matrices are linearized while accessing their elements. When all threads in a wrap access consecutive memory locations, the hardware coalesces, i.e., the hardware combines all these accesses into a combined access. Such access allows DRAM to deliver data as a burst.
For instance, in a row-major layout matrix, access to the input elements is already coalesced because consecutive threads will have access to consecutive elements of the column, as shown below:
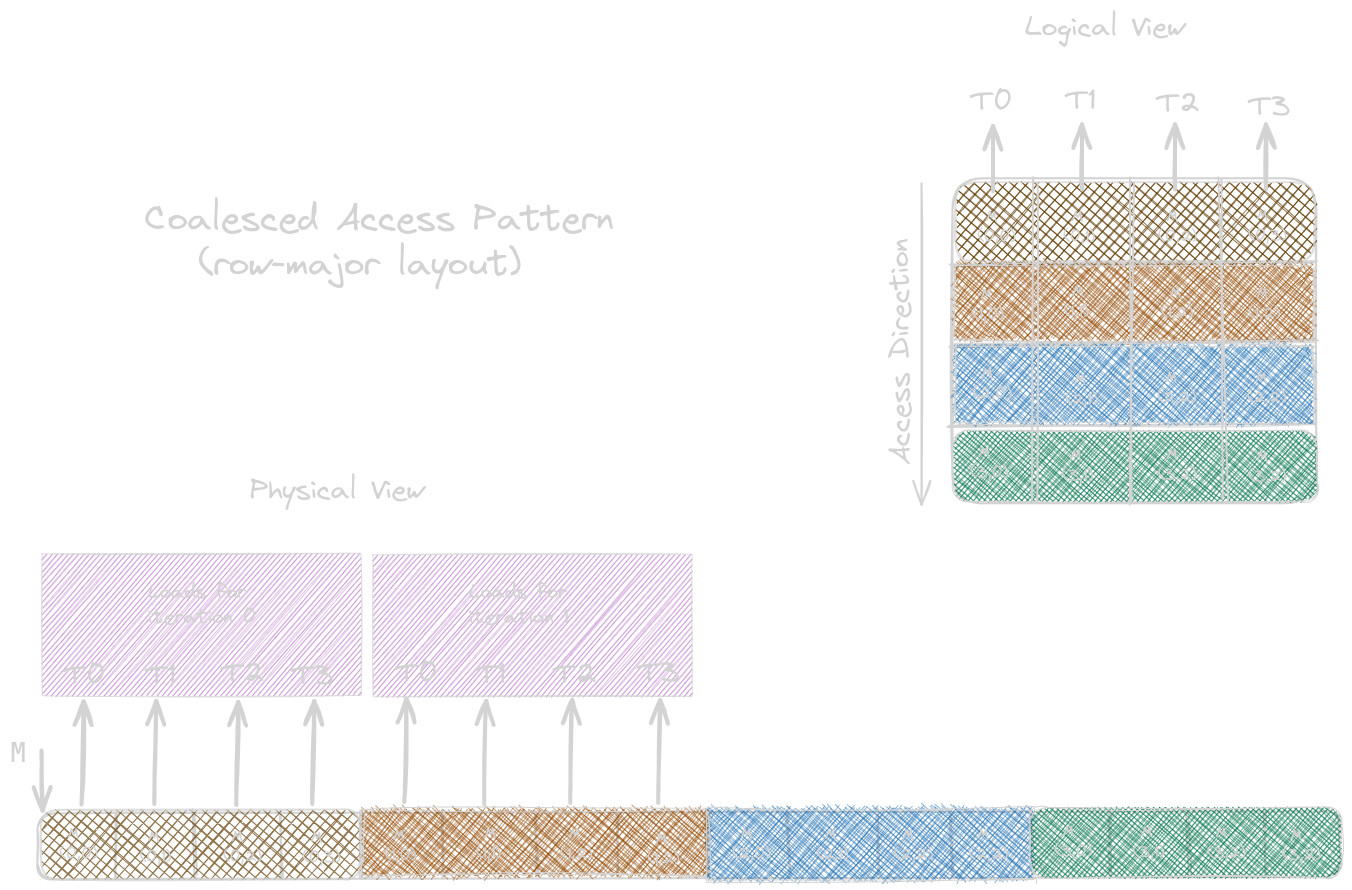
The next image, in a column-major layout matrix below, shows when the consecutive threads access the consecutive columns. The logical view of the matrix shows that it’s not favourable for coalescing. In the physical view, we are accessing consecutive elements, but they are not consecutive in memory because of the column-major layout.
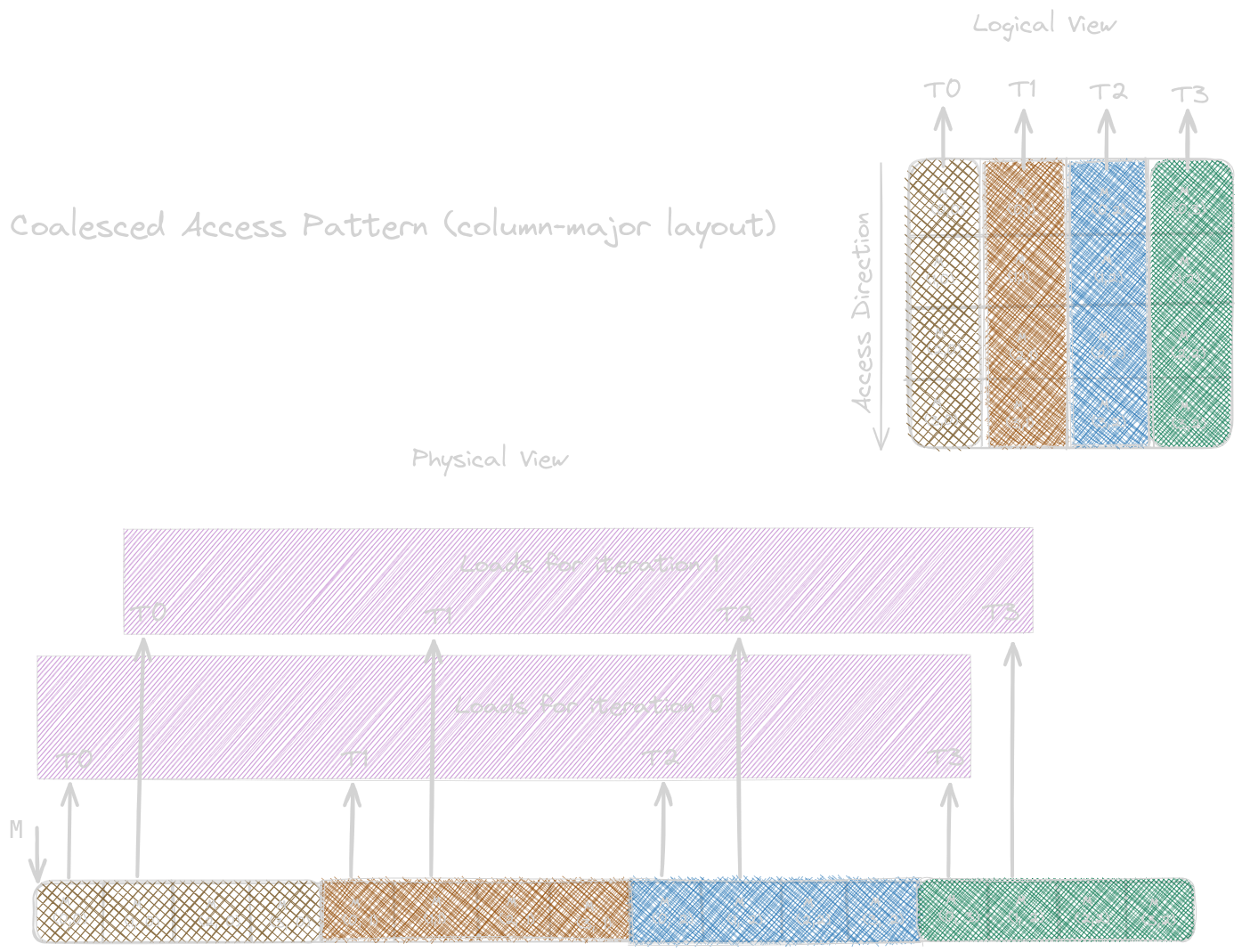
To optimize performance in cases where we cannot naturally achieve memory coalescing, we can rearrange how threads can be mapped to the data or rearrange the data layout itself. Another way is to transfer the data between the global memory and shared memory in a coalesced manner and carry an unfavourable access pattern in the shared memory for faster access latency.
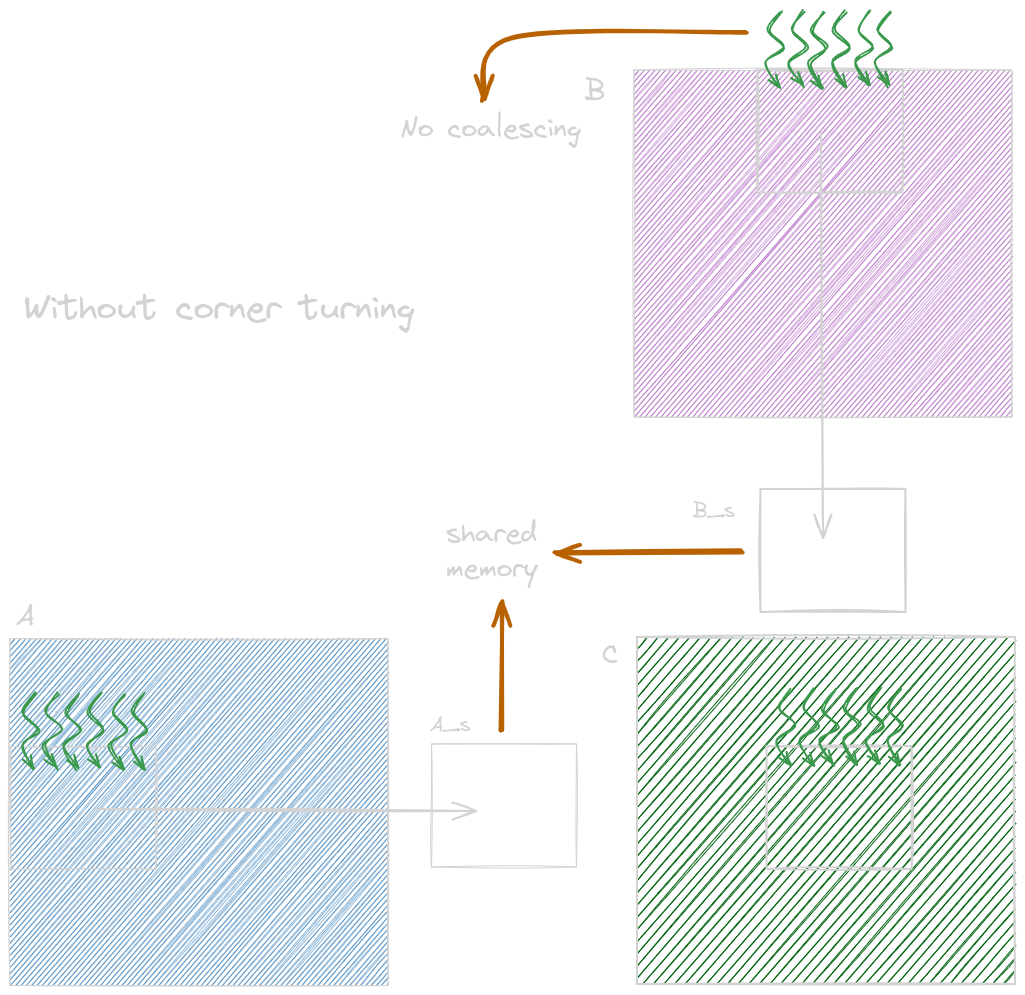
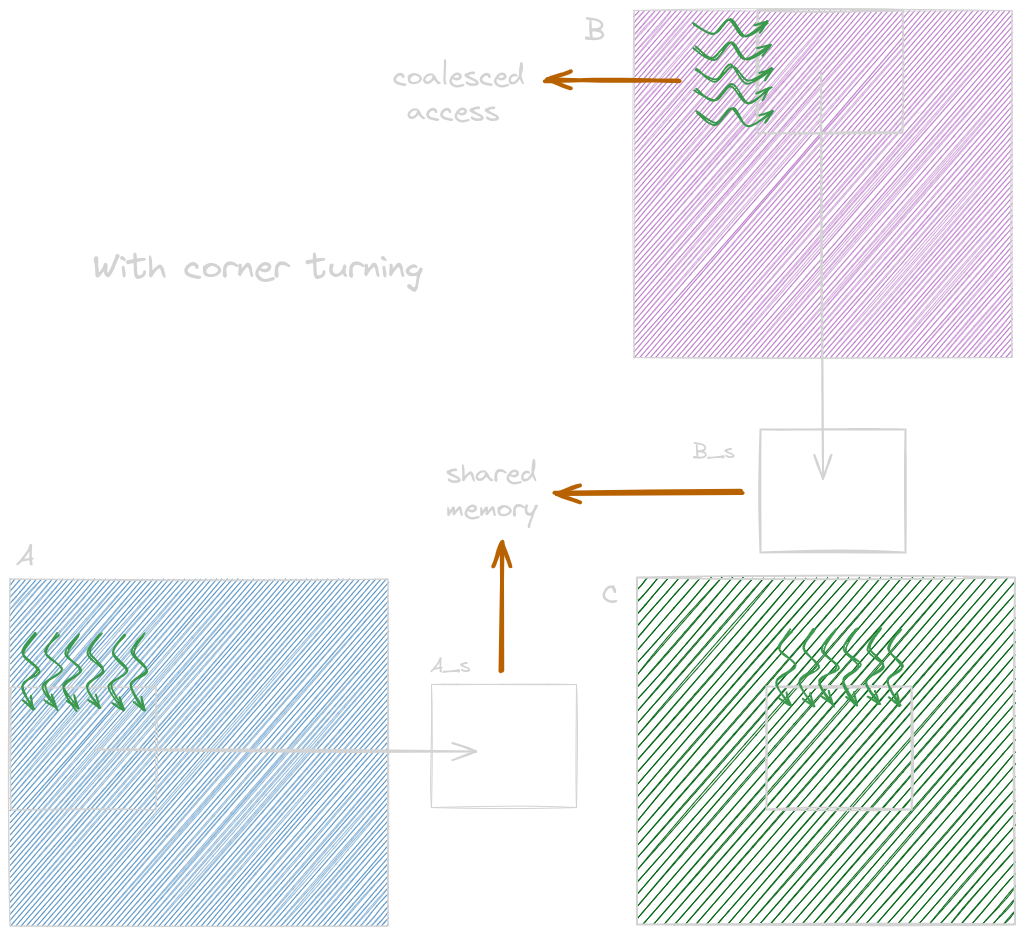
An optimization technique for a matrix-matrix multiplication when the second input matrix is in the column-major layout is known as corner turning. To solve this problem, where consecutive threads load nonconsecutive locations in the memory, resulting in uncoalesced memory accesses, we assign consecutive threads to load consecutive elements of the matrix (figure shown below). This ensures memory accesses are coalesced.
Matrix multiplication without corner turning.
Applying corner turning to coalesce accesses to matrix B (column-major layout).
Hiding Memory Latency
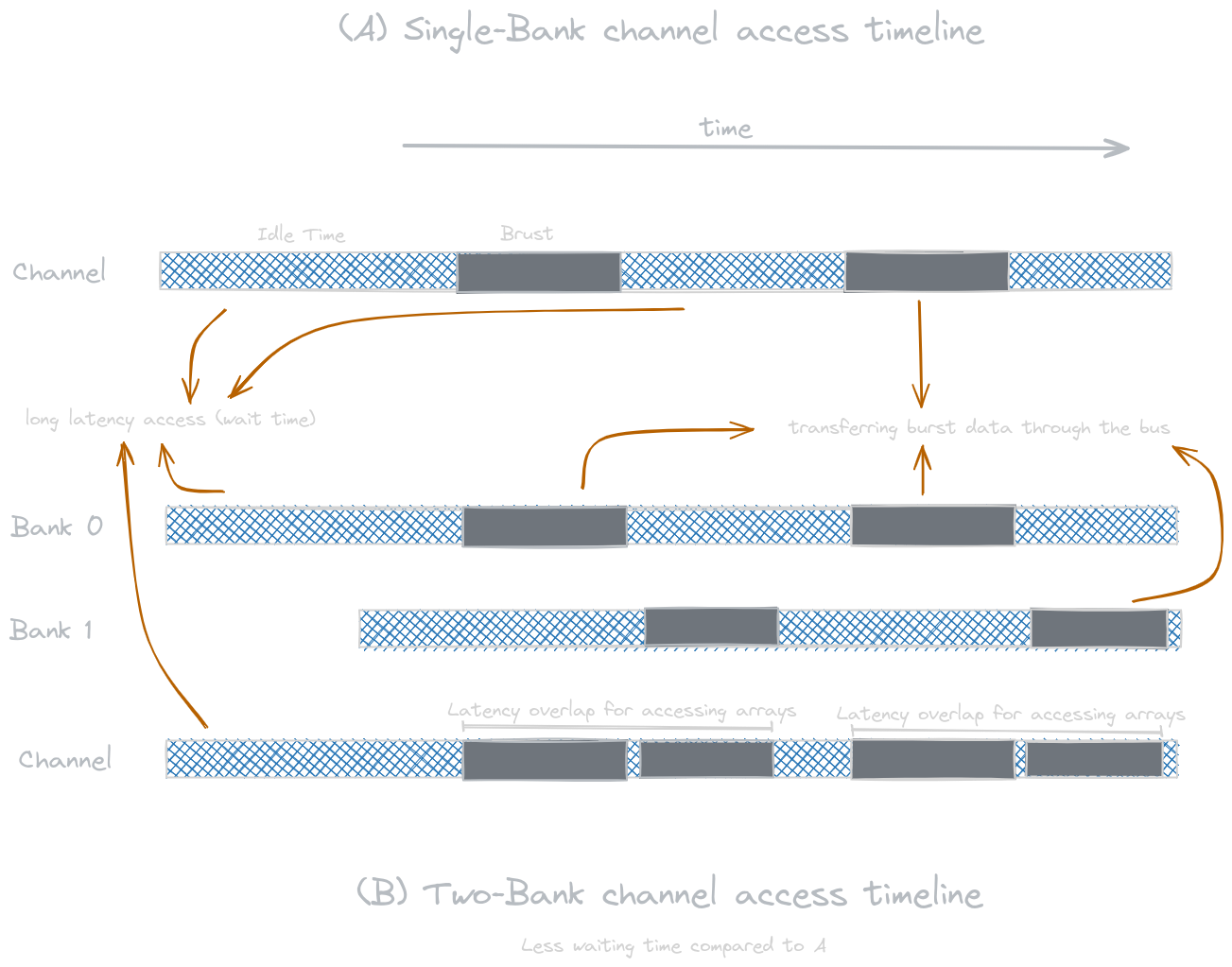
DRAM systems have two levels of parallel organizations: banks and channels. Each channel is a memory controller that connects DRAM banks to the processor. A bus connects the banks to the channels. A bus’s data transfer bandwidth is determined by its width and clock frequency. The image below shows the data transfer timing when a single bank and when two (or multiple) banks are connected to a channel and how to hide its latency.
Thread Coarsening
Until now, we have read about each thread executing the smallest unit of data and mapping each output element. However, this sometimes leads to redundant data loading by different threads, synchronization overhead, and other problems, especially when hardware serializes the work. To serialize the work, we can assign each thread multiple units of work. This process is known as thread coarsening.
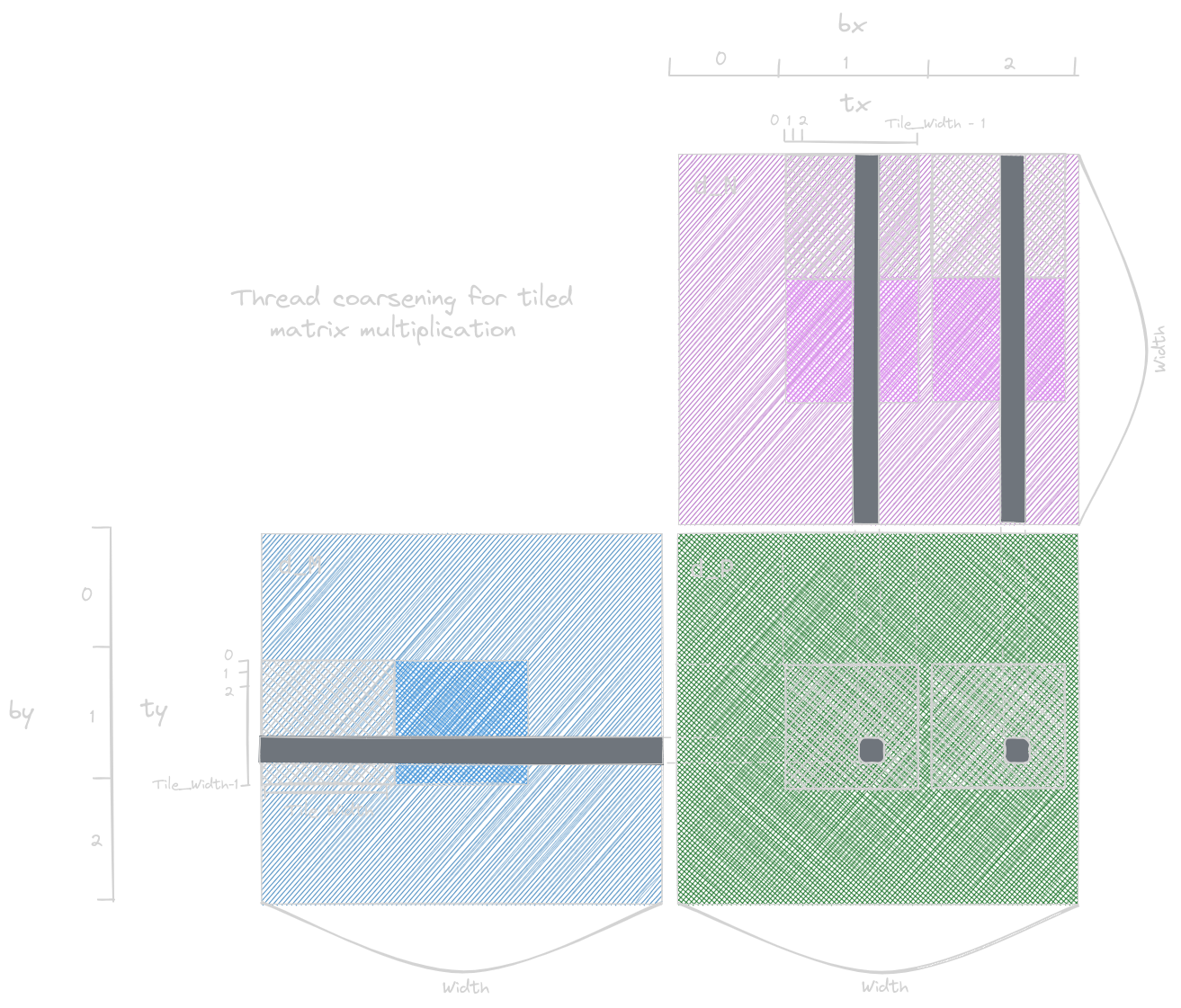
In the figure above, we load the same input files of matrix M with the two different input tiles of matrix N, which access two horizontally adjacent memory of the output tiles of matrix P. Note that here, we have different thread blocks loading the same input tiles. It’s the price we’ll pay to access two output tiles in parallel with different thread blocks. This process will be efficient only if these thread blocks run in parallel. This depends on whether the hardware serializes its process or not.
#define TILE_WIDTH 32
// number of original units of work responsible for each coarsened thread
#define COARSE_FACTOR 4
__global__ void matrixMulKernel(float* M, float* N, float* P, int width) {
__shared__ float Mds[TILE_WIDTH][TILE_WIDTH];
__shared__ float Nds[TILE_WIDTH][TILE_WIDTH];
int bx = blockIdx.x;
int by = blockIdx.y;
int tx = threadIdx.x;
int ty = threadIdx.y;
// Identify the row and column of the P element to work on
int row = by*TILE_WIDTH + ty;
int colStart = bx*TILE_WIDTH*COARSE_FACTOR + tx;
// Initialize Pvalue for all output elements
float Pvalue[COARSE_FACTOR];
for (int c = 0; c < COARSE_FACTOR; ++c) {
Pvalue[c] = 0.0f;
}
// Loop M and N to compute the P element
for (int ph = 0; ph < width/TILE_WIDTH; ++ph) {
// Collaborative loading of M tile into shared memory
Mds[ty][tx] = M[row*width + ph*TILE_WIDTH + tx];
for (int c = 0; c < COARSE_FACTOR; ++c) {
int col = colStart + c*TILE_WIDTH;
// Collaborative loading of N tile into shared memory
Nds[ty][tx] = N[(ph*TILE_WIDTH + ty)*width + col];
__syncthreads();
for (int k = 0; k < TILE_WIDTH; ++k) {
Pvalue[c] += Mds[ty][k] * Nds[k][tx];
}
__syncthreads();
}
}
for (int c = 0; c < COARSE_FACTOR; ++c) {
int col = colStart + c*TILE_WIDTH;
P[row*width + col] = Pvalue[c];
}
}
This is a powerful optimization technique, but there are several pitfalls we should keep a note of while applying:
- We should apply only when needed. For the cases discussed in the earlier blogs, we don’t need it, so we didn’t apply.
- Do not apply too much thread coarsening so that the hardware resources become underutilized.
- While applying thread coarsening, we should avoid increasing resource consumption to such an extent that it hurts the occupancy.
A Checklist of Optimization
Copied from the book1:
| Optimizations | Benefit to compute cores | Benefit to memory | Strategies |
|---|---|---|---|
| Maximizing occupancy | More work to hide pipeline latency | More parallel memory accesses to hide DRAM latency | Tuning usage of SM resources such as threads per block, shared memory per block, and registers per thread |
| Enabling coalesced global memory accesses | Fewer pipeline stalls waiting for global memory accesses | Less global memory traffic and better utilization of bursts/ cache lines | Transfer between global memory and shared memory in a coalesced manner and performing uncoalesced accesses in shared memory (e.g., corner turning) Rearranging the mapping of threads to data Rearranging the layout of the data |
| Minimizing control divergence | High SIMD efficiency (fewer idle cores during SIMD execution) | - | Rearranging the mapping of threads to work and/or data Rearranging the layout of the data |
| Tiling of reused data | Fewer pipeline stalls waiting for global memory accesses | Less global memory traffic | Placing data that is reused within a block in shared memory or registers so that it is transferred between global memory and the SM only once |
| Privatization | Fewer pipeline stalls waiting for atomic updates | Less contention and serialization of atomic updates | Applying partial updates to a private copy of the data and then updating the universal copy when done |
| Thread coarsening | Less redundant work, divergence, or synchronization | Less redundant global memory traffic | Assigning multiple units of parallelism to each thread to reduce the price of parallelism when it is incurred unnecessarily |
Where to Go Next?
I hope you enjoyed reading this blog post! If you have any questions or suggestions, please feel free to drop a comment or reach out to me. I’d love to hear from you!
This post is part of an ongoing series on CUDA programming. I plan to continue this series and keep things exciting. Check out the rest of my CUDA blog series:
- Introduction to Parallel Programming and CPU-GPU Architectures
- Multidimensional Grids and Data
- Compute Architecture and Scheduling
- Memory Architecture and Data Locality
- Performance Considerations
- Convolution
- Stencil
- Parallel Histogram
- Reduction
Stay tuned for more!
Resources & References
1. Wen-mei W. Hwu, David B. Kirk, Izzat El Hajj, Programming Massively Parallel Processors: A Hands-on Approach, 4th edition, United States: Katey Birtcher; 2022
2. Lecture 8: CUDA Performance Checklist; by Mark Saroufin; March 2024
3. I used Excalidraw to draw the kernels.
Let me know what you think of this article on Twitter @khushi__411 or leave a comment below!