GSoC Week 6! Adding Complex support nanvar and nanstd

int main() {
    [out = std::ref(std::cout << "Hello ")]() { out.get() << "World\n"; }();
}

Hehe, a bit of funnier hello! It was an amazing week during my GSoC internship! This blog post aims to discuss adding complex number support in nanvar and nanstd. I’ll first describe the current implementation, and then we’ll get into adding complex data type support to the function. I’ll also add small details you should know beforehand. Let’s start it. My PR: #6869.

Prerequite Knowledge

1. cupy.nanvar: Computes the variance along the specified axis, ignoring NaNs. By default, it calculates the variance of a flattened array.
2. cupy.nanstd: Computes the standard deviation along an axis, ignoring NaN values. It is defined by the square root of variance.

Formula:

1. Variance is given by:

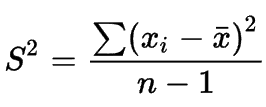
1. Standard Deviation is given by:

To know more about variance and standard deviation, you can read wikis’ great articles on Variance and Standard Deviation. I also recommend referring to CuPy’s documentation on cupy.nanvar and cupy.nanstd.

Implementation of nanvar and nanstd

nanvar and nanstd in CuPy are defined using ReductionKernels. _nanvar is called from the Pythonic function. nanvar and nanstd functions are defined here.

cpdef _ndarray_base _nanvar(_ndarray_base a, axis, dtype, out, ddof, keepdims):
    assert a.dtype.kind != 'c', 'Variance for complex numbers is not ' \
                                'implemented. Current implementation does not ' \
                                'convert the dtype'

    _count = _count_non_nan(a, axis=axis, keepdims=True)
    arrsum = _math._nansum(a, axis=axis, dtype=dtype, out=None, keepdims=True)

    if out is None:
        return _nanvar_core(
            a, arrsum, _count, ddof, axis=axis, keepdims=keepdims)
    else:
        return _nanvar_core_out(
            a, arrsum, _count, ddof, out, axis=axis, keepdims=keepdims)

The above function first counts the non-NaN values. This function is defined using create_reduction_func(). Here, CuPy developers have casted fp16, fp32, and fp64 to int64 data type. These values are then passed to _nanvar_core and _nanvar_core_out, where function parameters are declared as int64 _count or int64 ddof.

_count_non_nan = create_reduction_func(
    'cupy_count_non_nan',  # function name
    ('e->q', 'f->q', 'd->q'),  # fp16, fp32, fp64 : dtype supported
    ('isnan(in0) ? 0 : 1', 'a + b', 'out0 = a', None), 0)

The _nanvar function calls two other definitions, _nanvar_core and _nanvar_core_out. These are defined as ReductionKernels that call _nanvar_impl preamble. CuPy uses multiple template-type parameters to implement the preamble so that we can input two parameters with different data types. In T((x - mean) * (x - mean)) used below, templated arg, T is needed for explicit type conversion to support fp16 dtypes inputs.

cdef _nanvar_preamble = '''
template <typename S, typename T>
__device__ T nanvar_impl(S x, T mean, long long alpha) {
    return (isnan(x) ? T(0) : T((x - mean) * (x - mean))) / alpha;
}
'''

CuPy defines two ReductionKernel functions, _nanvar_core and _nanvar_core_out. The latter returns out arg. The S and T in nanvar_impl<S, T>() are the compile time arguments. These typenames help to make nanvar_impl<> dispatch different dtypes statically.

cdef _nanvar_core = ReductionKernel(
    'S x, T sum, int64 _count, int64 ddof',  # input params
    'S out',  # output params
    'nanvar_impl<S, T>(x, sum / _count, max(_count - ddof, 0LL))',  # map
    'a + b',  # reduce
    'out = a',  # post-reduction map
    '0',  # identity value
    '_nanvar_core',  # kernel name
    preamble=_nanvar_preamble  # preamble
)

cdef _nanvar_core_out = ReductionKernel(
    'S x, T sum, int64 _count, int64 ddof',  # input params
    'U out',  # output params
    'nanvar_impl<S, T>(x, sum / _count, max(_count - ddof, 0LL))',  # map
    'a + b',  # reduce
    'out = a',  # post-reduction map
    '0',  # identity value
    '_nanvar_core',  # kernel name
    preamble=_nanvar_preamble  # preamble
)

Add Complex dtype support

First, we removed the assertion implemented in the _nanvar definition to support complex dtype in nanvar and nanstd. We then added complex64 ('F') and complex128 ('D') dtypes as input: (Note: currently CuPy does not support ComplexHalf)

_count_non_nan = create_reduction_func(
    'cupy_count_non_nan',
    ('e->q', 'f->q', 'd->q', 'F->q', 'D->q'),
    ('isnan(in0) ? 0 : 1', 'a + b', 'out0 = a', None), 0)

At this point, CompileException is raised:

raise CompileException(log, self.src, self.name, options,
cupy.cuda.compiler.CompileException: /tmp/tmpatn3spsy/90a190cf40314048aa0bc41e71bb6f79257cd993.cubin.cu(48): error: no operator "/" matches these operands
            operand types are: const T / const long long

The error says the numerator and the denominator operands types are different as required by the operator/(). Initially, we thought to relax the inputs data types and support multiple templated arguments and modified the definition of operator/ to:

template <typename T, typename S>
__host__ __device__ inline complex<T> operator/(const complex<T>& lhs,
                                                const S& rhs) {
  return complex<T>(lhs.real() / rhs, lhs.imag() / rhs);
}

No doubt the tests passed locally, but CI is the boss. There were many internal failures that said we needed to change the declaration in the header files too. But since the complex support in CuPy is borrowed from the CUDA toolkit, thrust my mentor suggested not to change this but instead cast the divisors. We will get back to this point later. We need to make some more changes. But lets’ consider the above part for now and follow here.

At this point, there were two interesting problems to tackle.

1. Different dtypes returned

   E   AssertionError: ndarrays of different dtypes are returned.
   E   cupy: complex64
   E   numpy: float32
   

2. The type casting problem

   raise CompileException(log, self.src, self.name, options,
   cupy.cuda.compiler.CompileException: /tmp/tmpi3pra36j/b3738b71343a743f571053eac598f491c4fa0ce8.cubin.cu(43): error: no suitable conversion function from "T" to "_type_reduce" exists
   

Different data types of outputs were returned for all the cases that didn’t require the out variant. We discussed many possibilities and concluded to modify our implementation in the following way:

We need to define ReductionKernels explicitly for complex64 and complex128 when out=None because the data type of out in _nanvar_core is not user-defined. (This was my major missing part). Instead, when the out argument is given, we can tell the dtype of out as U out in _nanvar_core_out. Therefore we need to define kernels with input dtype as complex, when dtypes is complex64 or complex128 and out=None, while we do not need to change in the other case.

cpdef _ndarray_base _nanvar(_ndarray_base a, axis, dtype, out, ddof, keepdims):

    _count = _count_non_nan(a, axis=axis, keepdims=True)
    arrsum = _math._nansum(a, axis=axis, dtype=dtype, out=None, keepdims=True)

    if out is None:
        if a.dtype == cupy.complex64 or dtype == cupy.complex64:
            nanvar_core = _nanvar_core_complex64
        elif a.dtype == cupy.complex128 or dtype == cupy.complex128:
            nanvar_core = _nanvar_core_complex128
        else:
            nanvar_core = _nanvar_core
        out = nanvar_core(
            a, arrsum, _count, ddof, axis=axis, keepdims=keepdims)
    else:
        _nanvar_core_out(
            a, arrsum, _count, ddof, out, axis=axis, keepdims=keepdims)
    return out

We added a new nanvar_impl function inside the preamble definition to support complex dtypes. Similar to the above demonstration, we used multiple template args to implement this. We explicitly cast the x and mean too complex dtyes. In the implementation below, we use std::norm. To multiply with the conjugate of the number required for the multiplication of complex numbers.

cdef _nanvar_preamble = '''
# ... code here ...

template <typename S, typename T>
__device__ T nanvar_impl(complex<S> x, complex<T> mean, long long alpha) {
    return (isnan(x) ? T(0) : T(norm(x - mean))) / alpha;
}
'''

The concept mentioned above remains the same, except for the following changes:

• Two ReductionKernels are defined (one for complex64 and the other for complex128)
• Instead of using the templated parameters for input dtypes (x and sum), they are explicitly mentioned with complex64 and complex128
• We also explicitly specified the output dtype for complex64 is float32 while for complex128 is float64
• While the denominator (sum / _count) is cast to float and double. You can see the changes below.
• We also removed Compiletime arguments as they are confusing. Note that the type place holders S and T in <S, T> are different from template typenames typename S and typename T.

cdef _nanvar_core_complex64 = ReductionKernel(
    'complex64 x, complex64 sum, int64 _count, int64 ddof',
    'float32 out',
    'nanvar_impl(x, sum/static_cast<float>(_count), max(_count-ddof, 0LL))',
    'a + b',
    'out = a',
    '0',
    '_nanvar_core_complex64',
    preamble=_nanvar_preamble
)

cdef _nanvar_core_complex128 = ReductionKernel(
    'complex128 x, complex128 sum, int64 _count, int64 ddof',
    'float64 out',
    'nanvar_impl(x, sum/static_cast<double>(_count), max(_count-ddof, 0LL))',
    'a + b',
    'out = a',
    '0',
    '_nanvar_core_complex128',
    preamble=_nanvar_preamble
)

Yay! We now fixed all the AssertionErrors when out=None cases! Now lets’ get back to the point where I said we would talk later. We still got one CompileException error same as mentioned above when the out argument was given. Typecasting to T, using static_cast<T>() works fine.

cdef _nanvar_core_out = ReductionKernel(
    'S x, T sum, int64 _count, int64 ddof',
    'U out',
    'nanvar_impl(x, sum / static_cast<T>(_count), max(_count - ddof, 0LL))',
    'a + b',
    'out = a',
    '0',
    '_nanvar_core',
    preamble=_nanvar_preamble
)

Yey!! We did this! cupy.nanvar and cupy.nanstd now supports complex data types arguments as inputs!

Acknowledgement

I’d love to acknowledge Masayuki Takagi for guiding me with the concepts, for all the discussions, and for helping me with the errors. Thanks a ton to you!