GSoC Week 1! Implementing log_ndtr

Heya! I’m excited to share my first week’s experience with my mentor, the CuPy, and the GSoC via this blog post. Are you? It was a great week! Following the discussions made in the community bonding period, I started working on a special function, log_ndtr. I learned about the CuPy ufuncs, numerical stability & optimizing the algorithm, and off-course mathematical details about log_ndtr. Let’s get into the blog post to know more about it :)

Apart from log_ndtr, I worked on adding other special functions, expn PR: #6790 and logsumexp PR: #6773 that I believe are turning into an attractive shape. I’ll share more about them in my upcoming blog post. This post is for log_ndtr!

I’m planning to structure the post as follows:

1. About log_ndtr
2. Universal Functions
3. Numerical Stability of Algorithm
4. Performance Benchmarks
5. Acknowledgement

Let’s dig more …

About log_ndtr

log_ndtr calculates log of the area under the standard Gaussian cumulative distribution function. Mathematically, it is given by:

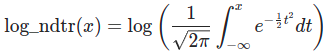
log_ndtr returns the area under the graph by operating the element-by-element in the given inputs. Such functions are known as universal functions—more on this in the next section.

Since log_ndtr is a universal function, we created a cupy.ufuncs to implement it and used the following algorithm:

static __device__ double log_ndtr(double x)
{
    double t = x * NPY_SQRT1_2;
    if (x < -1.0) {
        return log(erfcx(-t) / 2) - t * t;
    } else {
        return log1p(-erfc(t) / 2);
    }
}

Same for the single-precision version. I initially used the templated version, but my mentor guided me that single-precision versions are faster on GPU, hence recommended to calculate for both versions explicitly. And tada performance really improved a lot. If you want to see that, please click this link.

We implemented log_ndtr explicitly for floating-point numbers and double data type versions. I also added documentation and test for the same. Yey completed the PR, and this got merged! PR: #6776.

Welcome log_ndtr to the CuPy! Here’s how you can work on it:

>>> import cupy
>>> import cupyx
>>> from cupyx.scipy.special import log_ndtr
>>> x = cupy.array([4, 4, 12, 13])
>>> cupyx.scipy.special.log_ndtr(x)
array([-3.16717434e-05, -3.16717434e-05, -1.77648211e-33, -6.11716440e-39])
>>>

Universal Functions

Universal functions, a.k.a ufuncs, work on input element-by-element patterns. CuPy’s ufuncs are written in Cython. And supports broadcasting, type-promotion, and output type determinations similar to NumPy. You can check the official documentation for the same link here. Ufuncs are called by using create_ufunc defined at cupy/_core/_kernel.pyx.

cpdef create_ufunc(name, ops, routine=None, preamble='', doc='',
                   default_casting=None, loop_prep='', out_ops=None,
                   cutensor_op=None):
    ops_ = _Ops.from_tuples(ops, routine)
    _out_ops = None if out_ops is None else _Ops.from_tuples(out_ops, routine)
    return ufunc(
        name, ops_.nin, ops_.nout, ops_, preamble,
        loop_prep, doc, default_casting=default_casting, out_ops=_out_ops,
        cutensor_op=cutensor_op)

This functions calls the ufunc class defined here. We created a ufunc for log_ndtr as follows:

log_ndtr = _core.create_ufunc(
    'cupyx_scipy_special_log_ndtr',
    (('f->f', 'out0 = log_ndtrf(in0)'), 'd->d'),
    'out0 = log_ndtr(in0)',
    preamble=log_ndtr_definition,
    doc="""
    ....
    """
)

Here, the parameters of the ufuncs are:

• cupyx_scipy_special_log_ndtr: name of the function
• (('f->f', 'out0 = log_ndtrf(in0)'), 'd->d'): Input dtypes. It shows the float32 input will return float32 input and we will use the single precision version for the calculation. Second thing is it says float64 inputs will output float64 type and use the default type for its calculation.
• out0 = log_ndtr(in0): It’s the default output type.
• preamble=log_ndtr_definition: we wrote the definition of function explicitly in the function.
• doc: the documentation part.

Numerical Stability of Algorithm

This is an exciting part of this post. You might think, as the name suggests, log_ndtr, we could have implemented as log(ndtr). Have you thought? I thought so. Let me show you the pseudo-code of the algorithm using the above method.

if a > 6 do
    return -ndtr(-a)
if a > -20 do
    return log(ndtr)
else do
    calculate Taylor series approximation of erf to compute the log CDF

But this process has a major caveat. It has a high relative error in the interval [5, 6]. The error value immediately increases and then immediately falls. You can see the below visualization to create an image in your mind.

There’s a pretty good solution to this problem using erfc and erfcx functions to avoid loss of precision. SciPy’s work inspires this! Here are the mathematical details about the same: Some prerequisite formulas apart from log_ndtr’s formula that you should know before-ahead.

Let the CDF of the normal distribution be F(x), such that:

F(x) = erfc(-x/√2)/2
     = 1 - erfc(x/√2)/2

For values x < -1, to ensure high precision for large negative values erfc is replaced in by:

log F(x) = log(erfc(-x/√2)/2)
         = log(erfcx(-x/√2)/2)*exp(-x**2/2))
         = log(erfcx(-x/√2)/2) - x**2/2

For x >= -1, formula used is:

log F(x) = log(1 - erfc(x/√2)/2)
         = log1p(-erfc(x/√2)/2)

The above formula was beneficial and improved the stability of the algorithm. Here’s the plot of the stable version:

Pic Courtesy: SciPy gh-15172

Performance Benchmarks

The most crucial part! We focussed on the performance for our impl a lot. In a short summary, we implemented cupy.ufuncs for performance reasons. Secondly, and more importantly, we implemented single and double precision versions separately to get an advantage of GPU. We achieved approximately 30% faster speed for float32 than float64. Also, CuPy’s performance compared to SciPy’s performance is remarkable!

Here’s the benchmark …

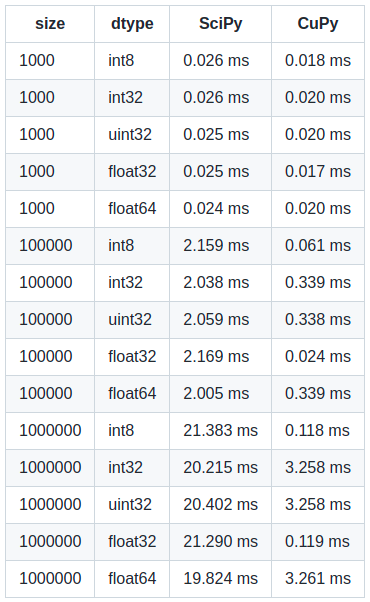
Please note my system configurations are NVIDIA GEFORCE GTX 1650Ti (4GB GDDR6 dedicated), Intel(R) Core(TM) i7-10870H CPU Model, and DDR4-2933, 16GB RAM model. You may get slightly different comparisons in your system.

Acknowledgement

I thank my mentor Masayuki Takagi for his guidance, for reviewing my work, and giving valuable suggestions to improve our implementation. It’s great connecting with you. Thank you!

I also want to acknowledge the SciPy team for their implementation; their work inspires this. Thank you, SciPy!